实现优先级队列最常用的数据结构是堆，堆的常见实现有二叉堆、斐波那契堆、二项堆等。

　　二叉堆

　　堆是一种完全二叉树，我们以小根堆为例，小根堆的性质就是，每个节点都小于其左孩子和右孩子，不难发现，这种二叉树，根的值是最小的。

　　堆有以下几种操作：堆的初始化、修改某个值（规定修改之后的值小于等于原来的值）、插入某个值、取出根节点（即取出该优先队列中的优先级最高的值）。

　　在进行这几种操作的时候，要维护堆的性质。

　　堆的存储

　　我们不难发现以下结论：在一棵完全二叉树中，假设节点下标从0开始，那么点i的左孩子的下标为 (i<<1)+1，右孩子的下标为(i<<1)+2 ，父节点的下标为(i-1)>>1，我么可以使用数组来存储这棵完全二叉树。

　　向下调整

　　向下调整即调整某个子树成为小根堆，由于小根堆的任意一个子树必定也是小根堆，当我们修改了位于i节点的某个值的时候，假设修改的值不小于原来的值，或者说修改的是根节点，那么如果要保持小根堆的性质，那么必定要判断这个节点是否需要移动，如果需要移动，那么必定是会移动到其子树中，不会向上移动。

　　所以这时候就要将这个节点和它的两个孩子中的值较小的进行交换，由于完全二叉树的性质，右子树的深度总是小于等于左子树，所以为了这一小点优势，我们通常在两个孩子值相同时，和右孩子交换，然后这时候和他交换的这个孩子又需要调整了，显然也需要向下调整，因此我们递归调用向下调整，直到没有交换，或者到了叶子节点。这个操作的时间复杂度为O (lgn) 。

　　向上调整

　　向上调整和向下调整一样，适合将某个节点的值改为比以前更小或者相等的值，或者修改了叶子节点的情况。

　　在这两种情况下，该节点需要向上移动，就是直接和这个节点的父节点比较，如果比父节点还小，那么就和他的父节点交换，然后递归向上调整它的父节点，直到到达根节点，或者某次没有交换。这个操作的复杂度也是O(logn)。

　　初始化

　　完全二叉树的一个显而易见的性质，假设其标号从0开始，到n-1结束，那么从n/2到n-1的点全是叶子节点，叶子节点可以看成是节点数为1的堆，所以说我们如果要构建一个堆，就从(n/2)-1到0点进行向下调整即可。

　　初始化的时间复杂度乍一看是O(nlogn) ，调整n/2次，每次复杂度是O (logn)，这不是O (nlogn) 吗？其实不然，调整n/2次不假，但是并不是每次调整都是O (logn) ，因为每次调整的复杂度取决于调整的子树的高度。

　　因此，其复杂度小于O (nlogn) ，实际上初始化堆的时间复杂度为O (n) 。

　　修改某值

　　假设把下标为i的节点的值改为了key（修改之后的值比之前的小，也就是优先级更高），那么如果要维护堆的性质，就要在该节点处向上调整。该操作的时间复杂度为O (logn)。

　　插入某值

　　将新节点插入到末尾，这个新节点必定是叶子节点，那么直接在这个节点上向上调整即可。该操作的时间复杂度为O (logn) 。

　　获取优先级最高的值并删除

　　由于二叉堆的性质，根节点的优先级必定是最高的（即节点的值最小）所以获取优先级最高的值只需要将根节点返回即可，如果要删除掉该节点，那么就将最后一个节点放到根节点的位置，然后从根节点处向下调整即可。该操作的时间复杂度为O(logn) 。

　　二叉堆实现代码

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class Heap<T extends Comparable<T>> {
    //堆的规模
    private int n;
    //具体的堆
    private List<T> a;
    public Heap(T[] a) {
        this.a = new ArrayList<>();
        this.a.addAll(Arrays.asList(a));
        this.n = this.a.size();
        build();
    }
    /**
     * 初始化堆
     */
    public void build() {
        for (int i = (n >> 1) - 1; i >= 0; i--) {
            down(i);
        }
    }
    /**
     * 获取父节点的下标
     * @param i
     * @return
     */
    private int parent(int i) {
        return (i-1)>>1;
    }
    /**
     * 获取左孩子的下标
     * @param i
     * @return
     */
    public int left(int i) {
        return (i << 1) + 1;
    }
    /**
     * 获取右孩子的下标
     * @param i
     * @return
     */
    public int right(int i) {
        return (i << 1) + 2;
    }
    /**
     * 向下调整，以满足小根堆的性质
     * @param i
     */
    public void down(int i) {
        int left = left(i);
        int right = right(i);
        int small = i;
        if (left < n && a.get(left).compareTo(a.get(i)) < 0) {
            small = left;
        }
        if (right < n && a.get(right).compareTo(a.get(small)) < 0) {
            small = right;
        }
        if (small != i) {
            T temp = a.get(i);
            a.set(i, a.get(small));
            a.set(small, temp);
            down(small);
        }
    }
    /**
     * 向上调整
     * @param i
     */
    public void up(int i) {
        int parent = parent(i);
        if (parent >= 0 && a.get(parent).compareTo(a.get(i)) > 0) {
            T temp = a.get(i);
            a.set(i, a.get(parent));
            a.set(parent, temp);
            up(parent);
        }
    }
    /**
     * 将下标为i处的节点值更新为key（变小）
     * @param i
     * @param key
     */
    public void update(int i, T key) {
        a.set(i, key);
        up(i);
    }
    /**
     * 插入新的节点key
     * @param key
     */
    public void insert(T key) {
        a.add(key);
        n++;
        up(n - 1);
    }
    /**
     * 获取并移除根节点
     * @return
     */
    public T getTop() {
        T result = a.get(0);
        a.set(0, a.get(--n));
        down(0);
        return result;
    }
    @Override
    public String toString() {
        return a.toString();
    }
    public static void main(String[] args) {
        Integer[] a = {16, 4, 10, 14, 7, 9, 3, 2, 8, 1};
        Heap<Integer> heap = new Heap<>(a);
        System.out.println(heap);
        heap.insert(13);
        System.out.println(heap);
        heap.update(3, 1);
        System.out.println(heap);
    }
}

　　斐波那契堆

　　斐波那契堆(Fibonacci heap)是堆中一种，它和二项堆一样，也是一种可合并堆，可用于实现合并优先队列。斐波那契堆比二项堆具有更好的平摊分析性能，它的合并操作的时间复杂度是O (1) 。

　　与二项堆一样，它也是由一组堆最小有序树组成，并且是一种可合并堆。与二项堆不同的是，斐波那契堆中的树不一定是二项树，而且二项堆中的树是有序排列的，但是斐波那契堆中的树都是有根而无序的。

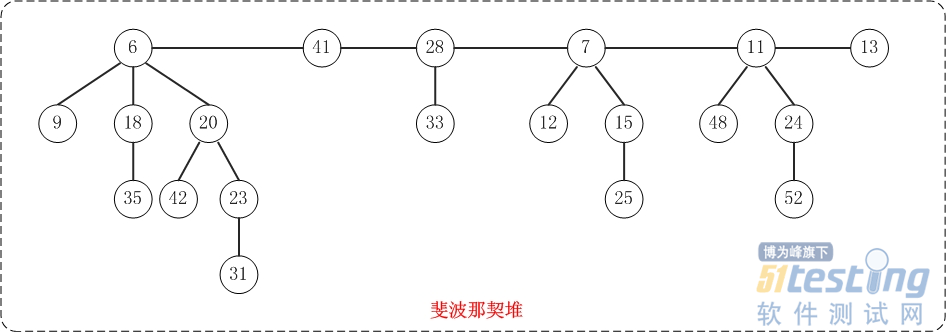
　　基本定义

typedef int Type;
typedef struct _FibonacciNode
{
    Type   key;                     // 关键字(键值)
    int degree;                     // 度数
    struct _FibonacciNode *left;    // 左兄弟
    struct _FibonacciNode *right;   // 右兄弟
    struct _FibonacciNode *child;   // 第一个孩子节点
    struct _FibonacciNode *parent;  // 父节点
    int marked;                     //是否被删除第1个孩子(1表示删除，0表示未删除)
}FibonacciNode, FibNode;

　　FibNode是斐波那契堆的节点类，它包含的信息较多。key是用于比较节点大小的，degree是记录节点的度，left和right分别是指向节点的左右兄弟，child是节点的第一个孩子，parent是节点的父节点，marked是记录该节点是否被删除第1个孩子(marked在删除节点时有用)。

typedef struct _FibonacciHeap{
    int   keyNum;                   // 堆中节点的总数
    int   maxDegree;                // 最大度
    struct _FibonacciNode *min;     // 最小节点(某个最小堆的根节点)
    struct _FibonacciNode **cons;   // 最大度的内存区域
}FibonacciHeap, FibHeap;

　　FibHeap是斐波那契堆对应的类。min是保存当前堆的最小节点，keyNum用于记录堆中节点的总数，maxDegree用于记录堆中最大度，而cons在删除节点时来暂时保存堆数据的临时空间。

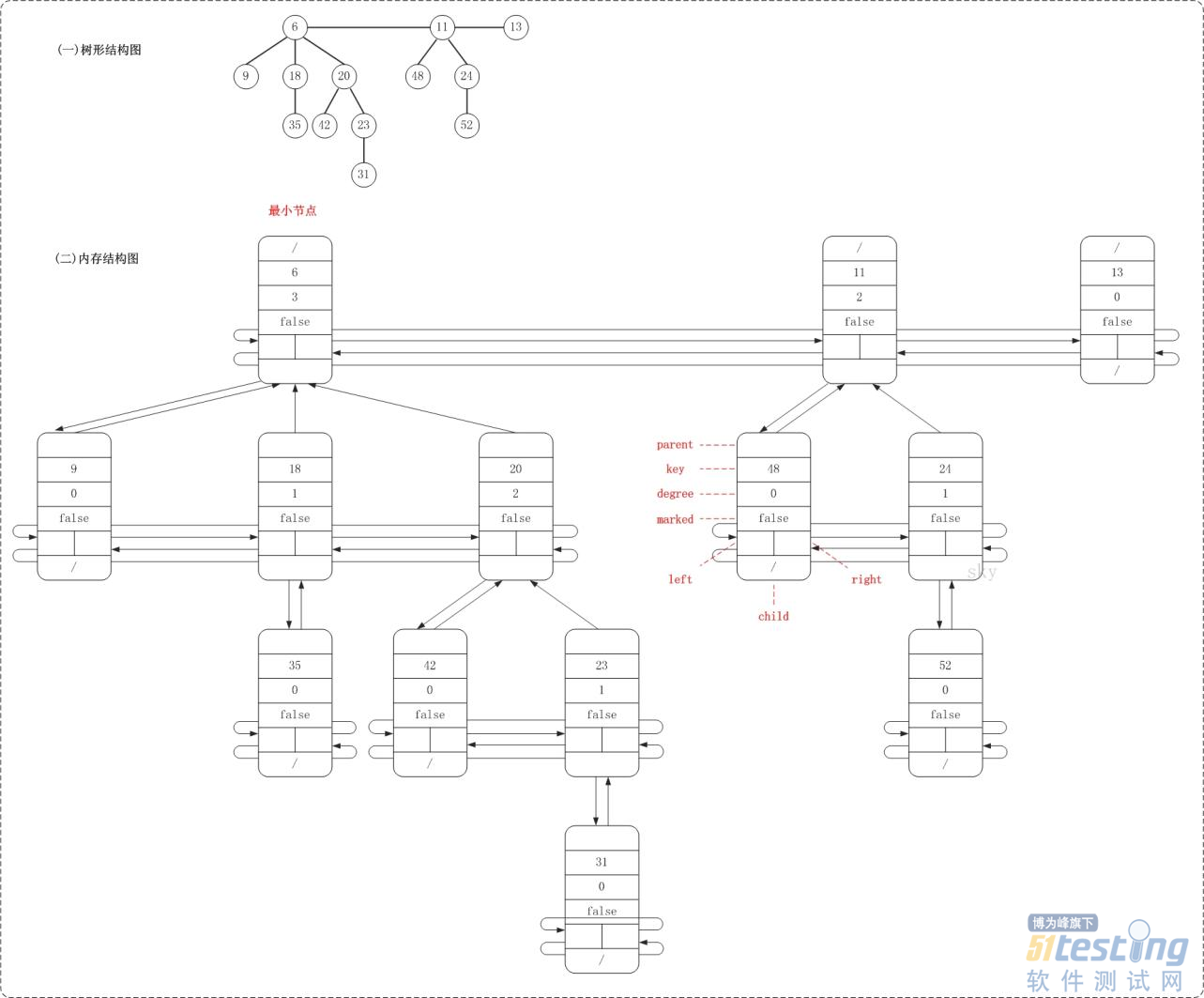
　　从图中可以看出，斐波那契堆是由一组小根堆组成，这些小根堆的根节点组成了双向链表(根链表)，斐波那契堆中的最小节点就是"根链表中的最小节点"！

　　基本操作

　　插入操作

　　插入操作非常简单：插入一个节点到堆中，直接将该节点插入到"根链表的min节点"之前即可；若被插入节点比"min节点"小，则更新"min节点"为被插入节点。

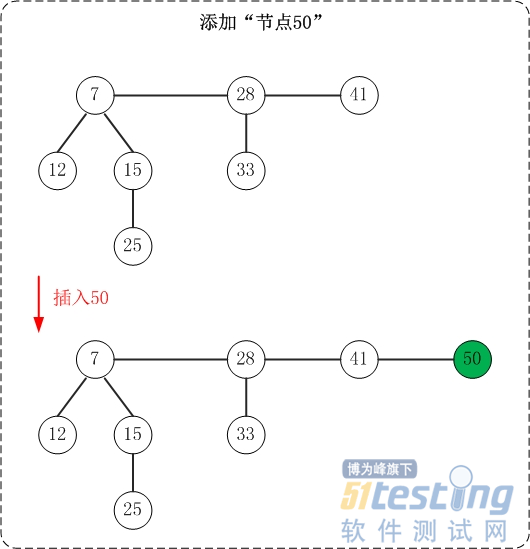
　　斐波那契堆的根链表是"双向链表"，这里将min节点看作双向联表的表头。在插入节点时，每次都是"将节点插入到min节点之前(即插入到双链表末尾)"。

　　此外，对于根链表中小根堆都只有一个节点的情况，插入操作就很演化成双向链表的插入操作。

/*
 * 将"单个节点node"加入"链表root"之前
 *   a …… root
 *   a …… node …… root
 *
 * 注意： 此处node是单个节点，而root是双向链表
*/
static void fib_node_add(FibNode *node, FibNode *root)
{
    node->left        = root->left;
    root->left->right = node;
    node->right       = root;
    root->left        = node;
}
/*
 * 将节点node插入到斐波那契堆heap中
 */
static void fib_heap_insert_node(FibHeap *heap, FibNode *node)
{
    if (heap->keyNum == 0)
        heap->min = node;
    else
       {
        fib_node_add(node, heap->min);
        if (node->key < heap->min->key)
            heap->min = node;
    }
    heap->keyNum++;
}

作者：中国农业银行研发中心西安研发部 陈登帅   

来源：http://www.51testing.com/html/62/n-4479462.html