- 一个二进制计数器教会我们平摊分析
一、平摊分析简介
平摊分析是算法研究中的一种常用思想。平摊分析中,执行一系列数据结构的操作所需要的时间是通过对执行的所有操作求平均而得出的。平摊分析可以用来证明在一系列操作中,通过对所有操作求平均之后,即使其中单一的操作具有较大的代价,但是其平摊代价还是很小的。平摊分析有三种常用技术,分别是聚集分析、记账方法和势能方法。
以上是平摊分析的学术介绍,也许看起来不够直观,不能瞬间秒懂,但是二进制计数器想必大家都有接触,今天就通过二进制计数器来学习平摊分析思想。
现在有一个数组A来实现二进制计数器的功能,数组A有K位,A[0]为最低位,A[k-1]是最高位,每一位取值可以为1或0,A可以用来表示0到2k-1间的任意整数。
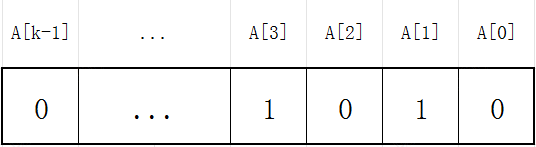
那么问题来了,假设二进制计数器A的初始状态为0,想要把A依次做加1操作,直至计数到n(n<2k),不考虑溢出情况,A所有二进制位总共要发生多少次翻转?
如果简单粗暴的考虑最坏情况,A每做一次加1操作,最多可能有k位发生翻转,那么A从初始状态0计数到n,总共需要做n次加1操作,则最多翻转nk次,所以复杂度为O(nk),但是用平摊分析去解决这个问题,答案并非如此,请看下文。
二、基于二进制计数器的平摊分析算法简析
2.1聚集分析法
A取1的时候,A[0]从0翻转为1,翻转1次;
A取2的时候,A[0]从1翻转为0,A[1]从0翻转为1,翻转2次;
A取3的时候,A[0]从0翻转为1,翻转1次;
A取4的时候,A[0]从1翻转为0,A[1]从1翻转为0,A[2]从0翻转为1,翻转3次;
...
更直观的,请看下图
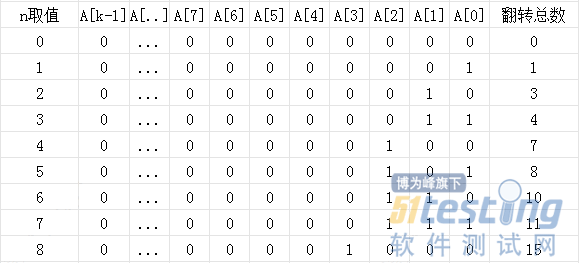
可以观察到,并不是每次加1操作所有二进制位都会翻转。聚集分析法,就是要确定n个操作序列的总代价的上界T(n),也就是最坏情况下为T(n),每个操作的平均代价为T(n)/n,这个平均代价也叫做平摊代价,即不管每个不同操作的实际代价是什么,它们都有相同的平摊代价。下面来求T(n)。
A[0]每次都要翻转,翻转n次;
A[1]每隔一次翻转,翻转n/2次;
A[2]每隔三次翻转,翻转n/4次;
A[3]每隔七次翻转,翻转n/8次;
...
那么二进制计数器累计加1直到n总共要做的翻转次数为
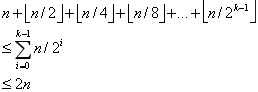
于是通过聚集分析方法可以得到,最坏情况下计数器A由0计数到n的操作时间T(n)=2n,每次操作的平摊代价为T(n)/n=O(1),作用于一个初始为0的二进制计数器上的n次加1操作的时间复杂度至多为O(n)。
2.2记账分析法
以上是用聚集分析方法来分析二进制计数器加1操作的复杂度。平摊分析还有另外一种常用的方法,叫做记账方法。在聚集分析法中,每次加1操作的平摊代价由总的代价平均而来,每次加1操作都有相同的平摊代价。但是在记账方法中,要给每一次加1操作分别定义平摊代价,现做如下定义:
由0翻转为1的实际代价为1;
由1翻转为0的实际代价为1;
由0翻转为1的平摊代价为2;
由1翻转为0的平摊代价为0;
由0翻转为1的平摊代价定义为 2,其中1用来支付翻转的实际代价,1用来作为该位上的“存款”,也就是说每出现一次由0翻转为1的操作,那么该二进制位上就会有1的“存款”,当该二进制位由1翻转为0时,就可以用这现有的“存款”1,去支付由1翻转为0的实际代价,因此由1翻转为0的平摊代价也相应定义为0。
基于以上定义,可以得到如下结论:
(1)对二进制计数器的每次加1操作,其平摊代价为2
二进制计数器加1操作通常由如下算法实现:
Increment(A)
{
i=0
While(i<k and A[i]==1)
{A[i]=0;i=i+1}
if (i<k)
{A[i]=1}
}也就是说从二进制计数器最低位开始,依次向高位查找,遇到1就将其翻转为0 ,直到遇到第一个0,将其翻转为1。在该过程中只会出现一次将0翻转为1,因此计数器A加1操作的平摊代价始终是2。
(2)A从初始状态0开始加1计数到任意n值,其平摊代价都是实际代价的上界
假设计数器A当前计数为n,对于A的任意一个二进制位,不管经历了多少次翻转:
若当前该二进制位为0,那么该二进制位上发生的平摊代价=实际代价;
若当前该二进制位为1,那么该二进制位上产生的平摊代价=实际代价+1。
由于计数器A二进制位为1的个数大于等于0, A不管计数在任何状态,其所发生的平摊代价总和始终是实际代价的上界。
于是通过记账方法可以得到,计数器A每次加1操作的平摊代价为2,由0计数到n的平摊代价T(n)=2n,作用于一个初始为0的二进制计数器上的n次加1操作的时间复杂度至多为O(n)。
2.3势能分析法
在记账方法中,如果操作的平摊代价比实际代价大,将“存款”与具体的数据对象关联,但是在势能分析法中,将这些“存款”与整个数据结构关联,所有的这样的“存款”之和,构成了数据结构的势能。如果操作的平摊代价大于操作的实际代价,则势能增加;如果操作的平摊代价小于操作的实际代价,要用数据结构的势能来支付实际代价,则势能减少。
在k位二进制计数器A计数问题中,做如下定义和假设:
(1)计数器A每一个二进制位由1翻转为0或由0翻转为1的实际代价为1;
(2)计数器A的势能为,为计数器A中1的个数。当A计数到n时,表示为,计数器A初始状态为0,=0;
(3)第i次加1操作的实际代价为,平摊代价为,=+-,第i次加1操作将个1翻转为0 ,,将1个0翻转为1,假设计数器不会溢出。
那么,可以得到如下分析结论:
(1)对A做任意n次加1操作,其平摊代价是实际代价的上界。证明如下:
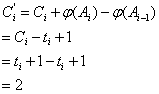
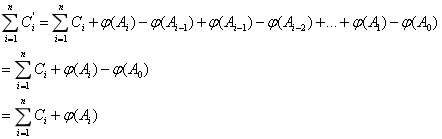
由于二进制计数器A在任意状态下1的个数都大于等于0,因此,于是对A做n次加1操作的平摊代价始终是实际代价的上界。
(2)计数器A每次加1操作的平摊代价为2
第i次加1操作将个1翻转为0,使得势能减少;将1个0翻转为1,使得势能增加1,于是有
于是通过势能分析方法可以得到,计数器A做n次加1操作的平摊代价T(n)=2n,复杂度为O(n),平摊代价为实际代价的上界,所以作用于一个初始为0的二进制计数器上的n次加1操作的时间复杂度至多为O(n)。
三、小结
本文以二进制计数器计数操作为例,用平摊分析中常见的聚集分析、记账方法、势能方法分析了其操作的复杂度。三种方法核心思想是一致的,都是计算出这一系列操作的平摊代价,证明平摊代价是实际代价的上界,从而得到实际的操作复杂度。但是三种方法又各有特点,聚集分析法通过计算所有操作序列的代价总和后再平均,对每一个操作,其平摊代价都是相同的;而记账分析法则是根据操作序列的特点,对每一个操作定义其平摊代价,每个操作的平摊代价各不相同;势能分析法的关键则是要为整个数据结构找到一个合理的势函数,势函数的定义决定了每个操作的平摊代价究竟会是多少。
平摊分析可以解决一个操作序列中有不同类型的操作,不同类型的操作的实际代价各不相同的问题,其核心在于,这一系列操作并不是完全独立的,而是存在关联关系,回顾记账分析法和势能分析法,对各个操作平摊代价的定义和势函数的定义恰恰就体现了不同操作间的内在联系。平摊分析可以应用于很多场景,如栈操作、动态表的扩张与收缩等等,我们将在后续继续学习。
版权声明:本文出自51Testing会员投稿,51Testing软件测试网及相关内容提供者拥有内容的全部版权,未经明确的书面许可,任何人或单位不得对本网站内容复制、转载或进行镜像,否则将追究法律责任。
- 0.00 查看剩余0%
- 【留下美好印记】赞赏支持
- 推荐阅读
- 换一换
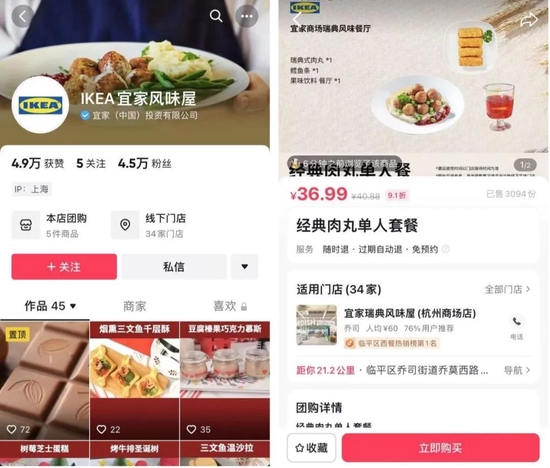
- 现在的宜家,越来越像美食UP主了。 大家对宜家最早的印象,无外乎是小红书千篇一律的极简风东欧性冷淡式家具,和特别适合拍照的线下门店。但在最近几年里,市场上来自宜家的声音越来越弱。 今年7月,“IKEA宜家风味屋”的抖音账号正式上线,该账号的认证主体为(宜家)中国投资有限公司,发布的视频以肉丸、牛排、松饼、各类蛋糕美食为主。IKEA宜家风味屋后续还尝试了直播带货,销量最高的是宜家瑞典风味餐厅的经典肉丸单人套餐,售价36.99元,目前已经迈出了3094份。 作为在中国布局多年的家居品牌来说,尝试美食视频可谓是破天荒的第一次,但也能看出宜家的窘迫处境。作为国际家居巨头,也需要通过线上的美食...
-
- 据 NYPost 报道,美国波音公司员工对美国国家航空航天局(NASA)决定派遣 SpaceX 的飞船来营救被困国际空间站(ISS)的宇航员感到“被羞辱(humiliated)”。 波音公司的星际客机(Starliner)因出现氦气泄漏和推进器故障,无法将布奇?威尔莫和苏尼?威廉姆斯安全送回地球。因此,NASA 决定使用 SpaceX 的龙飞船(Crew Dragon)来执行救援任务。 报道称,一位波音公司员工表示,这次事件是公司遭受的又一次打击,公司已经因为今年一系列商业飞行事故而受到外界强烈的批评。 “我们最近经历了太多尴尬的事情,成为了众矢之的。这次事件更是雪上加霜,”该员工说...
-
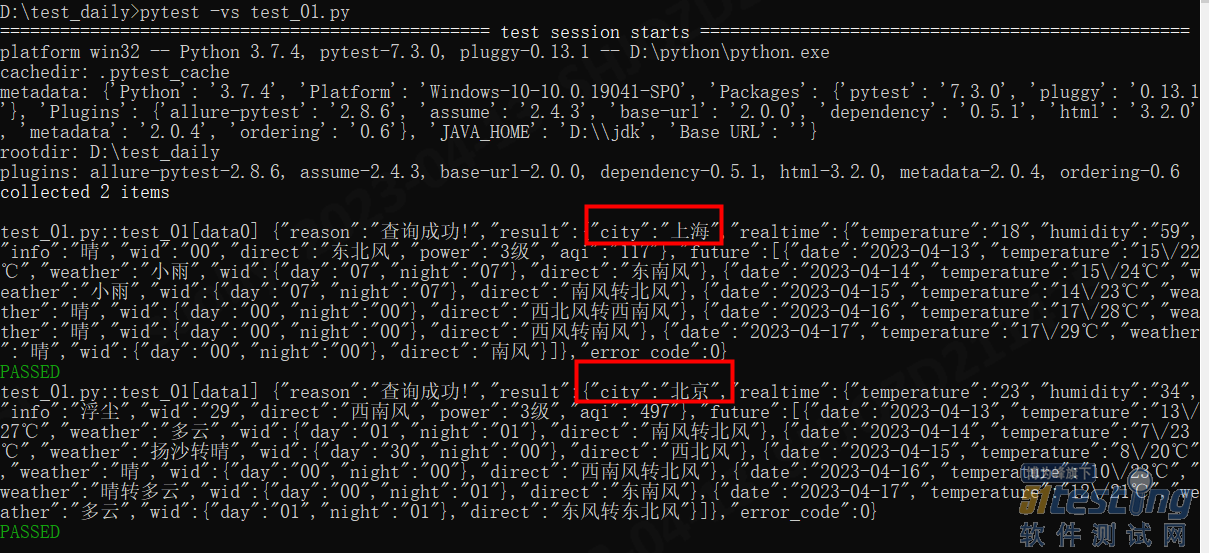
- 前言 无论什么自动化,部分测试用例均会运用到参数化,参数化可以帮助我们覆盖更多的测试用例,减少重复代码逻辑,然而自动化中也有多种实现参数化的方法,比如UnitTest的DDT模式,Pytest的fixture,以及Pytest的parametrize均可以实现测试用例的参数化。 今天小编介绍新的一种方法,通过hook函数来实现测试用例的参数化,废话不多说,直接进入正文。 pytest_generate_tests pytest_generate_tests钩子函数是Pytest框架中用来动态生成测试用例参数的钩子函数。通过它,我们可以在运行时动态地生成测试参数,从而避免手动编写重复...
-
- 性能压测是一种评估系统运行效率和稳定性的方法,通过模拟真实的使用场景和负载条件,对系统进行压力测试和负载测试,并对测试结果进行分析,以评估系统的性能,其中性能压测结果分析是性能压测的重要环节。以往的性能压测,测试执行和分析是分开的,分析的结果具有滞后性,且依赖于测试人员经验,存在分析标准不统一的问题。为解决上述问题,笔者探索了一个基于指标趋势和阈值规则的自动化异常分析方法,并将方法嵌入性能压测执行过程,实现实时、自动的捕获测试异常,帮助测试人员分析和评估系统在特定条件下的表现。 一、优化压测执行过程 性能压测执行过程一般由系统自动完成,无需人工参与,主要包含发压、数据聚合、结果汇总三个...
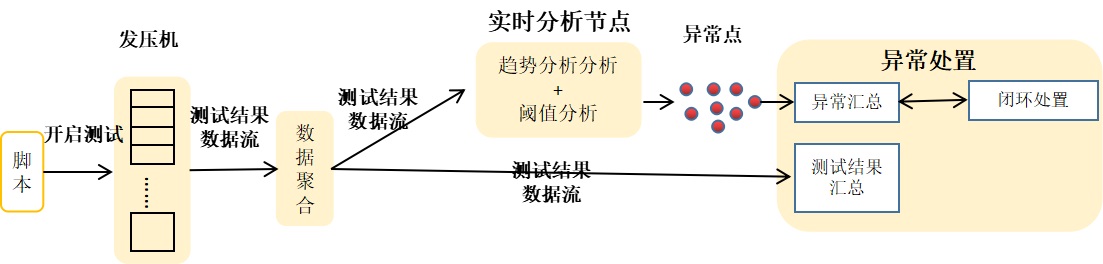
-
- 接口测试是测试系统组件间接口的一种测试。接口测试主要用于检测外部系统与系统之间以及内部各个子系统之间的交互点。测试的重点是要检查数据的交换,传递和控制管理过程,以及系统间的相互逻辑依赖关系等。 一、了解一下HTTP与RPC1. HTTP(HyperText Transfer Protocol) 说明:超文本传输协议,是互联网上应用最为广泛的一种网络协议。优点:就是简单、直接、开发方便,利用现成的http协议进行传输。流程图:2. RPC(Remote Procedure Call)说明:远程过程调用,它是一种通过网络从远程计算机程序上请求服务,而不需要了解底层网络技术的协议...
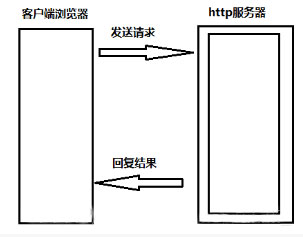
-
- 关于我们 联系我们 版权声明 广告服务 站长统计
- 建议使用IE 11.0以上浏览器,800×600以上分辨率,法律顾问:上海兰迪律师事务所 项棋律师
- 版权所有 上海博为峰软件技术股份有限公司 Copyright©51testing.com 2003-2024, 沪ICP备05003035号
- 投诉及意见反馈:webmaster@51testing.com; 业务联系:service@51testing.com021-64471599-8017

- 51testing软件测试圈微信



