命题

有一个处理单价为5角钱的饮料的自动售货机软件测试用例的设计。其规格说明如下：若投入5角钱或1元钱的硬币，押下“橙汁”或“啤酒”的按钮，则相应的饮料就送出来。若售货机没有零钱找，则一个显示“零钱找完”的红灯亮，这时在投入1元硬币并押下按钮后，饮料不送出来而且1元硬币也退出来；若有零钱找，则显示“零钱找完”的红灯灭，在送出饮料的同时退还5角硬币。

分析

根据命题可以分析出，自动售货机的业务中一共存在5个条件和5个结果，分别是：

条件：

1. 售货机有零钱找

2. 投入1元硬币

3. 投入5角硬币 

4. 押下橙汁按钮

5. 押下啤酒按钮 

结果： 

1. 售货机〖零钱找完〗灯亮    当售货机中没有零钱的时候就有亮红灯

2. 退还1元硬币                      当投入1元，而且售货机中没有零钱可找的时候

3. 退还5角硬币                      当投入1元，而且售货机中有零钱可找的时候

4. 送出橙汁饮料

5. 送出啤酒饮料

因果图－画条件和结果

因果图－画简单关系

在画完空白的条件和结果之后，可以将题目中最直接和简单的因果条件标出。

1. 条件“有零钱”和结果“红灯亮”是一个“非”的关系，当“有零钱”的时候，红灯是不亮的，而当售货机中“没有零钱”的时候，红灯必须要亮的。

2. 条件“投1元”和条件“投5角”是一个“E”的关系，这两个动作不可能同时发生，即同时投入1元钱和5角钱（不能同时为真）；但是我们允许即“不投入1元钱”也“不投入5角钱”（可以同时为假）。

3. 条件“选啤酒”和条件“选橙汁”是一个“E”的关系，这两个动作不可能同时发生，即同时“选择啤酒”和“选择橙汁”（不能同时为真）；但是我们允许即“不选择啤酒”也“不选择橙汁”（可以同时为假）。

4. 条件“选啤酒”和条件“选橙汁”对于程序处理过程是等价的，即二者无论是价格还是系统的处理方法都是相同的，因此这两个条件可以合并为一个中间节点。而且这两个条件之间使用“或”的关系。

5. 注意，条件“投1元”和条件“投5角”不是等价关系，表面上看，他们都是“钱”，好像差不多，但是对于程序的处理过程确实完全不同的，“投5角”后完全不用判断当前售货机中是否有零钱（因为题目中规定所有的商品都是5角钱），而“投1元”就不行了。

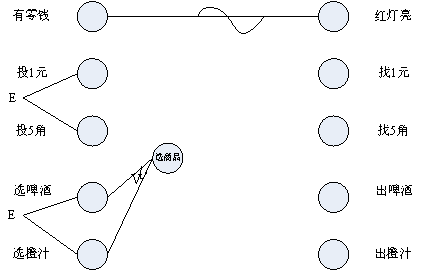
因果图－送出商品

现在我们从结果的角度考虑，要想“出啤酒”或者“出橙汁”，从现实买卖中分析必须要有什么先决条件呢？是的，就是“你的钱要付清”，而且你一定要选择了“啤酒”或者“橙汁”才行。而在上面的已有因果图中，我们无法找到“钱付清”的因素，因此这时候我们可以试着再加一个中间节点，就叫“钱付清”吧。

要想获得选中的商品，则条件“钱付清”和条件“选啤酒/选橙汁”必须要同时成立，因此是“与”的关系。

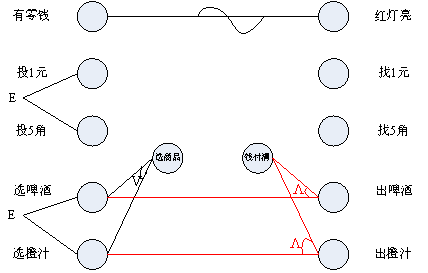
因果图－应该找零钱

根据题意，当投入1元钱，而且又选中了某一种商品的时候，系统是需要找零钱的。而现有条件和结果中并没有涉及到“应该找零钱”这种情况，因此我们还需要增加一个中间节点“应该找零钱”。

条件“投1元”和条件（中间节点）“选商品”与结果（中间）“应该找零钱”是“与”的关系，即这两个条件必须同时满足。

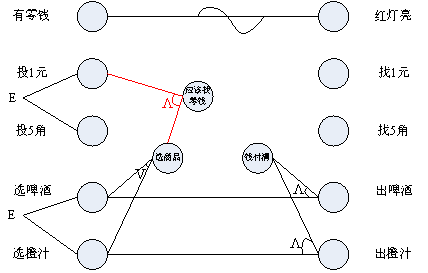
因果图－能够找零钱

上面已经确定了“投入1元钱”并且“选商品”，系统应该找给客户5角钱，那么接下来就要看当前售货机中是否有零钱可找了，庆幸的是，存在“有零钱”的条件；

现在系统“应该找零钱”给客户，而且恰恰又“有零钱”找给客户，那么就可以确定系统“能够找零钱”给客户了，所以这里我们又可以增加一个中间节点“能够找零钱”。

条件“有零钱”和条件（中间节点）“应该找零钱”与结果“能够找零钱”之间是“与”的关系。

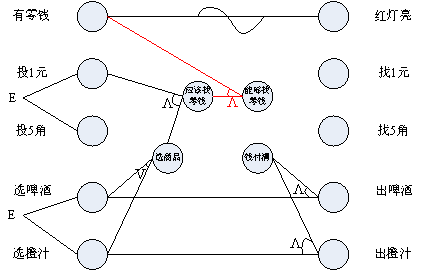
因果图－1元钱付清

现在已经确定客户“投入1元钱”并且“选商品”后，系统“有零钱”可找，那么紧接着就可以找钱给客户了。

条件“能够找零钱”和结果“找5角”是“恒等”的关系；

条件“能够找零钱”和结果（中间节点）“钱付清”也是“恒等”的关系；

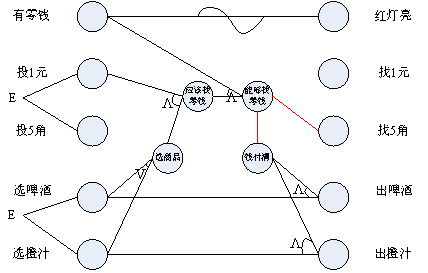
因果图－5角钱付清

考虑完投入1元钱后系统的处理情况，我们再来看投入5角钱后系统是如何处理的。因为售货机中的全部商品都是5角钱的，因此就不存在找零的问题了，只要客户“投入5角”并且按下相应的商品选择按钮就好了。

所以，条件“投5角”和结果（中间节点）“钱付清”直接是“恒等”的关系。

另外，条件“投5角”和条件（中间节点）“能够找零钱”都代表金额的计算已经结束，即“钱付清”，因此条件“投5角”和条件（中间节点）“能够找零钱”与结果（中间节点）“钱付清”之间是“或”的关系。

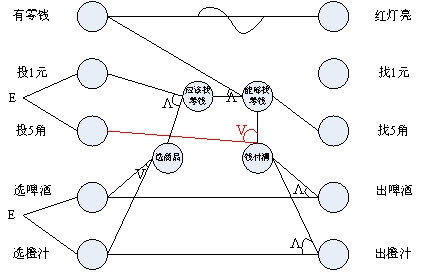
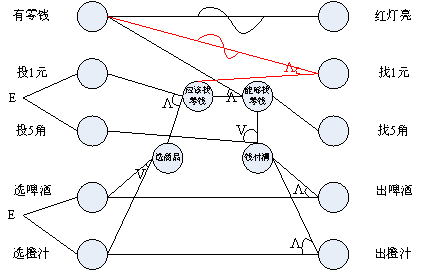
因果图－退还1元

我们考虑完了投入5角钱及投入1元钱并找零后，最后在考虑一下退还1元钱的情况。毫无疑问，当投入1元钱，并且选择了某种商品的时候，如果当前售货机中没有零钱可找，那么只能退还用户这1元钱了。

因此，条件“没零钱”和条件“应该找零钱”与结果“找1元”之间应该是“与”的关系，而且我们的条件中关于零钱是用了肯定的描述，即“有零钱”，要想表示没有零钱，直接使用一个“非”关就可以了。

判定表

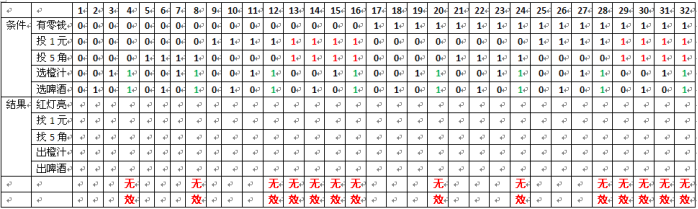
去除无效用例

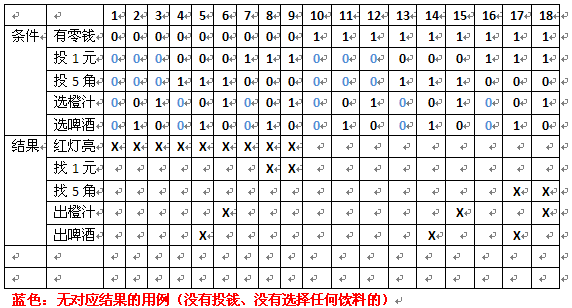
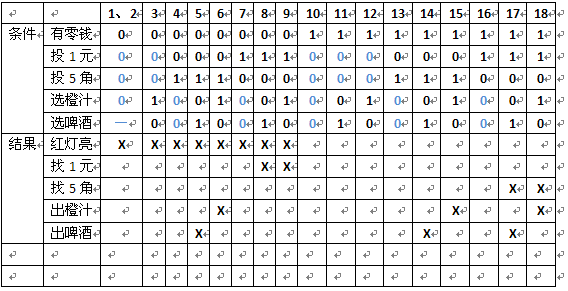
合并判定表

文章来源：百度文库