线性回归是机器学习中最基础的模型。虽然相较而言其结构简单且易理解，但其不仅能体现出机器学习重要的基本思想，还能构造出功能更加强大的非线性模型，对于后续机器学习算法的不断发展起了至关重要的作用。

　　在数理统计中，回归分析是确定多种变量间相互依赖的定量关系的方法。线性回归假设输出变量是若干输入变量的线性组合，并根据这一关系求解线性组合中的最优系数。在众多回归分析的方法里，线性回归模型最易于拟合，其估计结果的统计特性也更容易确定，因而得到广泛应用。而在机器学习中，回归问题隐含了输入变量和输出变量均可连续取值的前提，因而利用线性回归模型可以对任意输入给出对输出的估计。

　　1875年，从事遗传问题研究的英国统计学家弗朗西斯·高尔顿正在寻找父代与子代身高之间的关系。在分析了1078对父子的身高数据后，他发现这些数据的散点图大致呈直线状态，即父亲的身高和儿子的身高呈正相关关系。高尔顿将这种现象称为“回归效应”，并给出了历史上第一个线性回归的表达式：

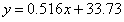
　　式中的y和x分别代表子代和父代的身高（单位为英寸）。回归效应在当今的机器学习中依然活跃。假定一个实例可以用列向量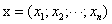表示，每个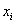代表了实例在第i个属性上的取值，线性回归的作用就是习得一组参数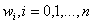使预测输出可以表示为以这组参数为权重的实例属性的线性组合。如果引入常量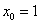，线性回归试图学习的模型就是：

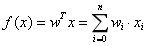
　　当实例只有一个属性时，输入和输出之间的关系就是二维平面上的一条直线；当实例的属性数目较多时，线性回归得到的就是n维空间上的一个超平面，对应一个维度等于n-1的线性子空间。

　　在训练集上确定系数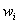时，预测输出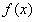和真实输出y之间的误差是训练模型的关键，这一误差以均方误差来定义。当线性回归的模型为二维平面上的直线时，均方误差就是预测输出和真实输出之间的欧式距离，也就是两点间向量的L2范数。使均方误差取得最小值为目标的模型求解方法就是最小二乘法，其表达式可以写成：

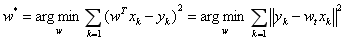
　　式中每个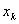代表训练集中的一个样本。在单变量线性回归任务中，最小二乘法的作用就是找到一条直线，使所有样本到直线的欧式距离之和最小。

　　从概率角度也可以解释，为何均方误差最小时的参数就是模型的最优参数。线性回归得到的是统计意义上的拟合结果，在单变量的情形下，可能每一个样本点都没有落在拟合得到的直线上。对这个现象的一种解释是回归结果可以完美匹配理想样本点的分布，但训练中使用的真实样本点是理想样本点和噪声叠加的结果，因而与回归模型之间产生了偏差，而每个样本点上噪声的取值就等于。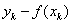

　　假定影响样本点的噪声满足参数为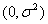的正态分布，这意味着取值等于0的噪声出现的概率最大，幅度越大的噪声出现的概率越小。在这种情形下，对参数w的推导就可以用极大似然估计理论完成，即在已知样本数据及其分布的条件下，找到使样本数据以最大概率出现的假设。

　　单个样本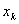出现的概率实际上就是噪声等于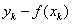的概率，而相互独立的所有样本同时出现的概率则是每个样本出现概率的乘积，其表达式可以写成：

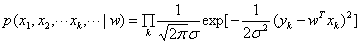
　　极大似然估计就是让以上表达式的取值最大化。出于计算简便的考虑，上面的乘积式可以通过取对数的方式转化成求和式，且取对数的操作并不会影响其单调性。经过一番运算后，上式的最大化就可以等效为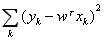的最小化。这和最小二乘法的结果一致。

　　因此，对于单变量线性回归而言，在误差函数服从正态分布的情况下，从几何意义出发的最小二乘法与从概率意义出发的极大似然估计是等价的。

　　确定了最小二乘法的最优性，接下来的问题就是如何求解均方误差的最小值。在单变量线性回归中，其回归方程可以写成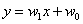。根据最优化理论，将这一表达式代入均方误差的表达式中，并分别对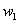和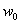求偏导数，令两个偏导数均等于0的取值就是线性回归的最优解，其解析式可以写成：

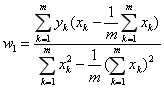
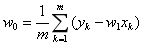
　　单变量线性回归只是一种最简单的特例。比如子代的身高并非仅仅由父母的遗传基因决定，营养条件、生活环境等因素都会产生影响。当样本的描述涉及多个属性时，这类问题就被称为多元线性回归。

　　多元线性回归中的参数w也可以用最小二乘法进行估计，其最优解同样用偏导数确定，但参与运算的元素从向量变成了矩阵。在理想的情况下，多元线性回归的最优参数为：

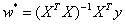
　　式中的X是由所有样本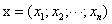的转置共同构成的矩阵。但这一表达式只在矩阵的逆矩阵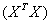存在时成立。在大量复杂的实际任务中，每个样本中属性的数目甚至会超过训练集中的样本总数，此时求出的最优解就不是唯一的，解的选择将依赖于学习算法的归纳偏好。

　　但不论采用怎样的选取标准，存在多个最优解都是无法改变的事实，这也意味着过拟合的产生。更重要的是，在过拟合的情形下，微小扰动给训练数据带来的毫厘之差可能会导致训练出的模型谬以千里，模型的稳定性也就无法保证。因此在构建线性回归模型时，要考虑过拟合的问题。最常用的方法就是给模型增加正则化项，限制参数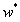的取值范围，从而提升模型的泛化能力。

作者：赵嘉铭 李志伟 赵旭   

来源：51Testing软件测试网原创