性能测试是描述测试对象性能相关特征并对其进行评价而实施的一类测试，是软件测试的重要组成部分，对于保证软件质量起到了至关重要的作用。TPS指单位时间完成的事务数，是衡量服务器承载能力的重要指标，直接体现软件系统性能的承载能力。TPS在性能测试中常作为重点关注的性能指标，目标TPS的计算需要一套科学客观的方法。

　　一、目标TPS的估算

　　当前在软件性能测试中估算目标TPS通常都会考虑被测系统未来一段时间的预期交易量，然而对于未来预期交易量往往是项目组凭借主观经验估计一个业务年增长率来进行估算的，缺乏科学客观的预测方法。

　　因此，我们提出了一种应用时间序列分析中的ARIMA模型估算被测软件未来预期日交易量，从而进行TPS分析的方法。该方法通过提取被测软件一段时间内生产上的交易量数据，建立ARIMA模型估算未来一段时间的交易量，为软件性能测试制定目标TPS提供科学客观的数据支撑。

　　二、未来交易量的预测方法

　　基于预测模型的软件性能测试TPS分析方法主要包括数据获取、描述性分析、数据预处理、模型训练、模型检验和交易量预测共六个主要步骤（如图1所示）。具体分析过程如下：

　　步骤S1：获取数据。因时间序列受滞后期影响，模型效果与序列长度有关，条件允许情况下应获取较多数据。获取被测软件在一段连续时间内（两个季度以上）生产上的日交易量。如获取被测软件连续n天的日交易量，得到一个n维列向量(X1, X2, X3, ... , Xn)T。

　　步骤S2：描述性分析。分析日交易量数据的基本特征，包括最大值、最小值、分位数等，以日期为横轴、日交易量为纵轴做序列曲线图，可视化展示日交易量数据序列，并观察数据变化趋势。

　　步骤S3：季节性判断。根据步骤S2中序列曲线图判断交易量数据是否具有季节性，若曲线图中每间隔λ个时间单位后交易量数据呈现出相似性，如都处于波峰或波谷，或都处于上升或下降，称序列有长度为λ的季节特性。如部分金融系统交易量表现出每周7天的周期特征。

　　步骤S4：数据预处理。主要为缺失数据处理和数据量级处理。

　　缺失数据处理。当某天的日交易量数据缺失时需进行数据填充，可分为以下三种情况：

　　1) 缺失值若出现在选取交易量时间段的开始和结尾，可直接删除这几天的数据；

　　2) 缺失值出现在序列中间且日交易量数据不存在季节性（季节性通常指年、季度、月、周、节假日等引起的数据周期性改变，具有固定的周期长度），则用缺失值附近3到5天的日交易量的均值进行填充。如第j(j<n)天的日交易量数据Xj缺失，可用附近5天交易量数据填充，Xj=(Xj-1+Xj-2+Xj-3+Xj-4+Xj-5) / 5。

　　3) 缺失值出现在序列中间且日交易量数据存在季节性，则用其他不同季节周期相同位置的日交易量的均值填充。设日交易量数据序列共有α个季节周期，季节性周期为λ，如果第β（1≤β≤α）个季节周期中的第j(j<n)天的日交易量数据Xj缺失，则：

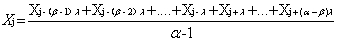
　　数据量级处理。当日交易量数据量级在千万级以上时则取自然对数降低数据量级，即将步骤S1中的n维列向量(X1, X2, X3, ... , Xn)T变换为(lnX1, lnX2, lnX3, ... , lnXn)T。

　　步骤S5：季节性数据序列的因素分解。若数据序列具有季节性，则需要进行因素分解。因素分解是将原始序列分解成趋势项T、季节项S、随机项I，可用加法或者乘法分解，加法分解：Y=T+S+I，乘法分解：Y=T*S*I。当步骤S2中序列曲线图显示的季节变动大致相等，即时间序列图等宽变化时，应采用加法分解。当骤S2中序列曲线图显示的季节变动与长期趋势大致成正比时，应采用乘法模型。

　　步骤S6：自相关、偏自相关分析。根据自相关图、偏自相关图初步确定序列是AR（自回归）序列还是MA（移动平均）序列，初步确定滞后阶数lag，即前期序列对后期影响的时间长度。如果自相关、偏自相关系数在最初的lag阶明显大于两倍标准差，lag阶之后的95%自相关、偏自相关系数在两倍标准差范围之内，且自相关、偏自相关系数衰减较快，初步确定滞后阶数为lag。

　　步骤S7：平稳性判断。通过ADF单位根检验平稳性。时间序列平稳性指序列均值、方差是与时间无关的常数，协方差与时间间隔有关，与时间无关的常数。若因素分解后的趋势项不平稳，则进行差分运算，直到差分后的序列平稳，同时记录差分阶数d。若因素分解后的趋势项平稳，步骤S8中的模型参数差分阶数d为0。差分运算是时间序列后期值减去前期值，记：

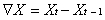
记为：

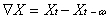
　　ω步差分，t为时间。

　　步骤S8：确定模型参数。ARIMA模型参数(p, d, q)，d是差分阶数，在步骤S7确定，p是交易量数据自相关滞后阶数，q是随机扰动影响交易量数据的滞后阶数。通过设定p、q变化范围，比如p的范围为1, 2, ... , p，q的范围为1, 2, ... , q，p、q应大于步骤S6中确定的lag阶数。循环迭代每一个(p, d, q)组合，建立一共p*q个ARIMA(p, d, q)模型，得到每一个模型的BIC统计量，共p*q个BIC统计量，BIC=m * ln(n) - 2ln(L)，其中m为模型参数个数，n为样本数，L为似然函数。构建一个p行q列的BIC值矩阵，对BIC排序找出最小BIC所在的行数和列数即为p、q。

　　BIC矩阵如下：

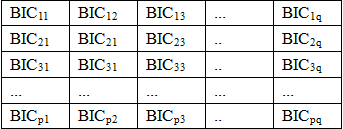
　　步骤S9：建立ARIMA(p, d, q)模型。差分阶数d由步骤S7确定，滞后阶数p、q由步骤S8确定。

　　步骤S10：分析评价模型。分析模型残差，通过LB统计量检验残差是否白噪声，若为白噪声，信息提取较充分，不为白噪声，可将p、q设置为步骤S6得到的滞后阶数lag尝试模型，也可设置为步骤S8得到的p、q附近值尝试模型。

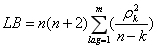
　　其中，n为残差序列长度，k为残差滞后阶数，ρk为残差自相关系数。

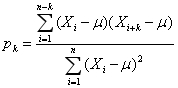
　　μ为残差序列的均值。

　　步骤S11：预测未来交易量X和TPS。输入需要预测的未来时间长度，用ARIMA模型预测未来交易量。根据预测结果计算TPS，按照二八原则，TPS=0.8X / (0.2H*60*60)，H为系统每天发生业务的小时数。

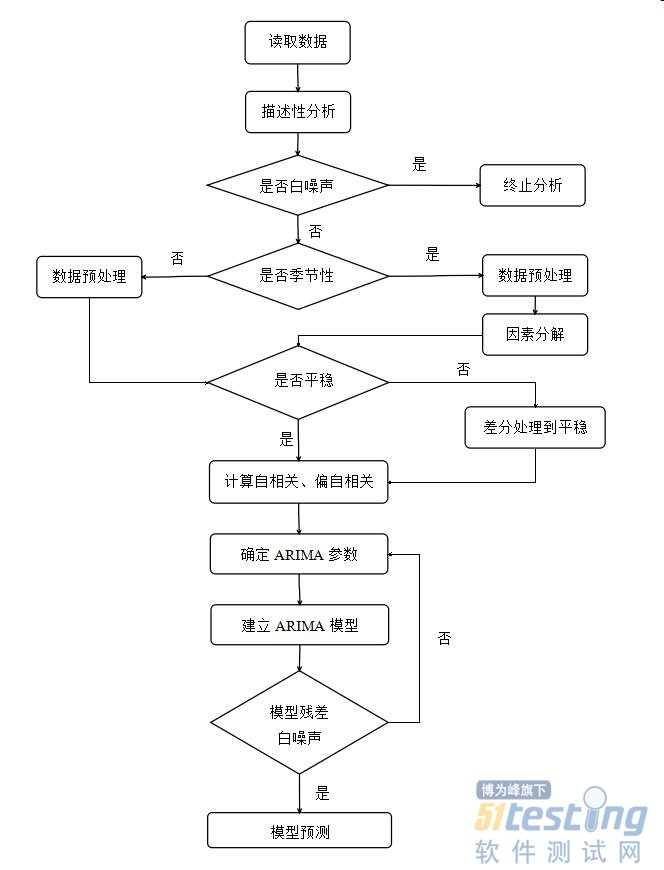
图1 基于ARIMA预测模型的软件性能测试TPS分析方法流程示意图

　　三、总结

　　基于ARIMA模型的软件性能测试TPS分析方法，合理利用了已经产生的数据资产，应用时间序列分析方法预测未来交易量，进行性能测试目标TPS的计算，具有科学性和客观性。并且，该方法不依赖具体的系统和需求，只依赖交易量数据，无需其他特征数据，具有很好的适用性和推广价值。

作者：赵晓彬   

来源：51Testing软件测试网原创